Exercises
 : shows the complete answer. |  : gives a hint |
 : plays a video solution |  : shows just the final answer |
 : these are important examples that illustrate new concepts, you should be sure to review the solutions to these questions | |
Exercises
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Find the point on the line $y=mx+b$ that's closest to the origin in terms of $m$ and $b$.
Icons courtesy of icons8.com
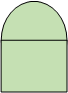
A rectangle whose base is on the x-axis is inscribed in the circle $x^2 + y^2 = 1$. What dimensions give the rectangle with the largest area?
Find the point on the line $y=mx+b$ that's closest to the origin in terms of $m$ and $b$.
$$\left(\frac{-mb}{1+m^2},\frac{b}{1+m^2}\right)$$
A piece of wire of that's 10" long is cut into two pieces. One is formed into a circle and the other into a square. How long should the two pieces be so that the total area is a minimum?
Let $x$ be the length of the piece used for the circle and $10 - x$ be the length of the piece used for the square. This makes the total area
$$A(x) = \pi x^2 + (10 - x)^2$$Differentiating that and setting the derivative equal to 0 gives us
$$A'(x) = 2\pi x + 2(10 - x)(-1)$$ $$2\pi x -20 + 2x = 0$$ $$(2\pi + 1)x - 20 = 0$$ $$x = \frac{20}{1 + 2\pi}$$The area formula is a quadratic function with a positive leading coefficient so it opens up which means this point must be a local minimum. This amkes the two piece lengths
$$\text{circle: }r = \frac{20}{1 + 2\pi}, \text{square: }s = 10 -\frac{20}{1 + 2\pi} = \frac{20\pi - 10}{1 + 2\pi} $$Suppose you have 53 square inches of material and you need to build a box with a square base and no lid that maximizes its volume. What would be the box's dimensions assuming all of the area goes into the sides?
$$\frac{\sqrt{53}}{3} \text{ in. } \times \frac{\sqrt{53}}{3} \text{ in. } \times \frac{\sqrt{159}}{6} \text{ in. }$$
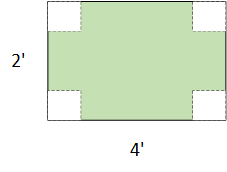
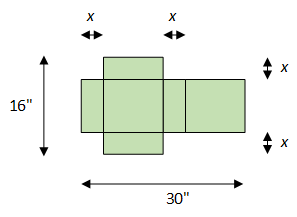
A 2' by 4' rectangular sheet has squares cut out at each corner. The sides are then folded up to form a box. What size squares will give a box with the maximum area.
0"
Find the equation of the line through the point $(2, 6)$ that cuts off the smallest area in the first quadrant.
$$y = -3x + 12$$
A cylinder needs to be made by cutting a rectangular piece and a circular piece (for the bottom) from a rectangular piece of metal that's 60 inches long and has no limit on its height. When the rectangular piece is rolled to form the sides, it has to fit exactly on the circular part. What dimensions will maximize the cylinder's area?
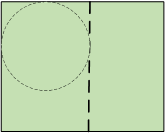
rectangle: 20" x 40π"
Two cars are moving toward an intersection on perpendicular roads. One car is heading south and the other west. The south bound car is 1 mile from the intersection and going 30 mph; the west bound car is 1.25 miles from the intersection and going 25 mph. At what time is the distance between the cars a minimum?
$$t\approx 0.0401 \text{ hours} \approx 2.406 \text{ minutes}$$
Tom is in a boat 10 miles from the shore and 20 miles from a dock. If the boat travels 7 mph and he can walk 2.5 mph, at what point between his current position and the dock should he land the boat so that his total travel time is a minimum?
The best course is just to sail directly to the dock.
The vertical distance traveled by a projectile is given by $d=\frac{2v_0^2\cos\theta\sin\theta}{g}$ where $g$ is the rate of acceleration due to gravity, $v_0$ is the initial velocity and $\theta$ is the angle at which the projectile is launched. If both $g$ and $v_0$ are constant, what angle will give the maximum range.
$$\theta = 45 ^\circ$$
The intensity of a sound is equal to the power of the source divided by the square of the distance from the source. Suppose two sound sources, one with a power of 10 watts and another with a power of 40 watts are 2 meters apart. How far from the first source on the line between the sources is the total intensity a minimum?
$$\frac{2}{\sqrt[3]{2}+1} \text { meters}$$
The kinetic energy of an object of mass $m$ moving at a velocity $v$ is given by $K = \frac{mv^2}{2}$. A test rocket has an initial mass $m$ and accelerates at a constant rate $a$. As the rocket flies it's mass decreases at a constant rate $bt$ as it uses up its fuel. At what time is the rocket's kinetic energy at a maximum?
$$t = \frac{m}{2b}$$
The force between two electrical charges is proportional to the product of their magnitude and inversely proportional to the square of the distance between them. If a positive charge with magnitude 10 units is 2 meters from a negative charge of 5 units. At what point between the two charges will a particle with a positive charge of 4 units experience the minimum force?
$$x = \frac{2\sqrt[3]{2}}{\sqrt[3]{2} + 1} \text{ from the positive 10 unit source}$$
Suppose the cost of producing $x$ units $C(x) = .1x^3 + 20x + 1000$ where $x$ and $C$ are both in thousands. Find the production level that minimizes the average cost.
The average cost is given by
$$\bar{C} = \frac{C(x)}{x} = \frac{.1x^3 + 20x + 1000}{x} = .1x^2 + 20 + \frac{1000}{x}$$ $$\bar{C}' = .2x - \frac{1000}{x^2}$$ $$.2x - \frac{1000}{x^2} = 0$$ $$.2x^3 - 1000 = 0$$ $$.2x^3 = 1000$$ $$x^3 = 20000$$ $$x = \sqrt[3]{20000} \approx 27.144$$The original average cost function is quadratic and opens up so this must be a local minimum. This means that the minimum average cost occurs when the production level is 27,144 units.
